APLICACIÓN DE UN MODELO DE TEORÍAEVOLUTIVA DE JUEGOS EN PROCESOS DE COOPERACIÓN

Abstract

This paper is an approach of computational methods of complexity, particularly evolutionary game theory applied in processes of human cooperation. the cocoa producers and stockholders of the municipality of Palermo, located in Huila Colombia were considered. This is an apllied, descriptive and non-experimental study, wish focus in the producers and stockers of cocoa of the municipality. in the development of this sttudy, interviews were conducted and direct observation was exercised, in order to determine strategic attitudes. After performing a computational simulation of strategic attitudes of those involved through an iterated prisoner dilemma tournament, it was concluded that the formulation and execution of cooperation strategies, framed in a constant communication between the parts, the improvement of relations and the reciprocity will generate a mutual benefit for both; the cocoas producers and the stockists.

Introducción

Considerando que, en los últimos tiempos, los modelos matemáticos y computacionales han sido usados para facilitar el desarrollo económico y social, así como para resolver diversos problemas presentes del entorno, la teoría de juegos, ofrece útiles herramientas para la modelación y la optimización de procesos que involucran interacción social en general.

Por otra parte, diversos estudios sobre este ámbito, han demostrado que la mayoría de situaciones sociales, son juegos de suma no nula y que, por tanto, los jugadores involucrados en un determinado juego, pueden perder o ganar simultáneamente dado un escenario. Esto, ha permitido permite discernir que la cooperación es más conveniente que la deflexión en un contexto estratégico en el que se quiera actuar de manera racional (Colman, 2003; Yuksel, 2017).

En este sentido, se considera a los productores y acopiadores de cacao del municipio de Palermo ubicado en el departamento del Huila - Colombia, tomando en cuenta que, actualmente, hay aproximadamente 700 Hectáreas sembradas y un total 222 agricultores especializados en la producción de cacao, estando considerada como una de las actividades económicas más importantes del municipio y un motor propio de su crecimiento económico y desarrollo social.

El objetivo principal del estudio estuvo encaminado a que, por medio de la aplicación de la teoría de juegos, se pudiese determinar la actitud estratégica más conveniente entre los productores y los acopladores de cacao del municipio de Palermo-Huila, en miras de promover la cooperación en los procesos comerciales de las partes. Así mismo, este estudio se presenta como un acercamiento de los modelos computacionales y matemáticos discretos al comportamiento social y económico.

El presente artículo sintetiza la formulación de actitudes de cooperación entre los productores y los acopiadores de cacao del municipio de Palermo por medio del uso de un modelo de teoría evolutiva de juegos, basado en el clásico dilema del prisionero. Se parte, de una revisión teórica de los conceptos más importantes del campo de la teoría de juegos, para seguidamente, profundizar en aspectos metodológicos del estudio. Finalmente se exponen unas conclusiones, las cuales establece la actitud estratégica más propicia para establecer, como ya se expuso, acciones oportunas que favorezcan la cooperación entre jugadores.

Aspectos teóricos

Teoría deJuegos
Enmarcada en el contexto de las matemáticas discretas, la teoría de juegos se encarga del estudio de modelos matemáticos que describen el conflicto y la cooperación entre entes inteligentes que toman decisiones. Tales decisiones se consideran estratégicas, es decir, que los entes que participan en el juego actúan teniendo en cuenta las acciones que tomarían los demás (Rodriguez, 2005) siendo las decisiones individuales resultantes de lo que un jugador espera que los otros jugadores hagan (Monsalve, 2003).

Para (Straffin, 2004) un juego es aquella situación en la que:

Existen por los menos dos jugadores.
Cada jugador tiene un número posible de estrategias o acciones las cuales puede elegir.
La estrategia elegida por cada jugador determina un resultado en el juego.
Dados los resultados, cada jugador obtiene unos pagos.

Los pagos representan el valor del resultado de los diferentes jugadores.

Juegos de suma no nula y el dilema del prisionero
En un juego de suma no cero o de suma no nula, los intereses de los jugadores no son estrictamente opuestos y por tanto, en el juego se puede combinar aspectos competitivos con algunas oportunidades de negociación. Las posibles acciones de competencia y cooperación, radican en las posibilidades de comunicación y coordinación que se le permite a los jugadores, y por tanto, a medida que estas posibilidades se den, los juegos pueden tener Importante elementos cooperativos que favorezcan a los distintos jugadores involucrados (Ricart, 1988).

Así mismo, el dilema del prisionero, un problema clásico dentro de la teoría de juegos, el cual ha sido aplicado en campos del conocimiento como la economía, la biología o la administración (Henrik & Broman, 2017) permite modelar diversas situaciones estratégicas en las que los jugadores deben optar por tomar una actitud estratégica cooperativa o no cooperativa. El modelo clásico del dilema del prisionero, se expresa en la matriz de pagos, figura 1.

Figura 1.
Matriz de pago. Fuente: elaboración Propia

Considerando que T > R > P > S.
Como se puede apreciar, si los jugadores deciden cooperar entre ellos, van a obtener una recompensa (R), pero, si un jugador decide cooperar y el otro lo traiciona, quien coopera obtendrá en pago del bobo (S) y el traidor mayor pago dentro del juego (T) (Li, Ma, Mei , Tian, & Stanley, 2017) considerando esto, la solución clásica del dilema del prisionero se da cuando los jugadores deciden no cooperar obteniendo un pago P. Si bien es cierto, y como ya se expuso con anterioridad, la cooperación entre las partes (pago R) es, en un sentido empírico, la actitud estratégica más conveniente para los jugadores, considerando que R>P.

Teoría evolutiva de juegos
En décadas recientes, surgió la teoría de evolutiva de juegos, la cual, por medio de métodos inspirados en biología, ha tratado de explicar situaciones de conflicto y cooperación entre jugadores. La Teoría Evolutiva de juegos nace como una interacción entre la ecología y la economía (Karl, 2011) siendo, además, un importante campo dentro de las matemáticas y la biología computacional (Adami, Schossau, & Hintze, 2016).

(Villena & Villena, 2005) señalan que en los últimos años, desde la publicación del libro Evolution and the Theory of Games, del biólogo John Maynard Smith, la teoría evolutiva de juegos ha empezado a captar la atención de muchos economistas que cuestionan la idea de agentes perfectamente racionales como único supuesto válido para estudiar el comportamiento económico humano, en ese sentido, enfatizan en el concepto de estrategia evolutivamente estable desarrollado por Smith, en el que se dice que una estrategia (fenotipo) evolutivamente estable es robusta a las presiones de la selección evolutiva en un sentido exacto. El marco típico en que se aplica este concepto es aquel donde se extraen repetidamente individuos de una gran población para que jueguen un juego simétrico de dos personas. En este orden de ideas, la estrategia evolutivamente estable, se debe entender como un refinamiento del concepto de equilibrio de Nash. Villena y Villena Expresan que “pese al criterio de estabilidad evolutiva se basa en ideas de la biología, es posible argumentar que también proporciona un criterio relevante de robustez para el comportamiento humano en una amplia variedad de situaciones que incluyen muchas interacciones en el contexto económico” (P.24).

Por su lado, Axelrod (1986) en su obra titulada la Evolución en la Cooperación plantea el siguiente problema: ¿En qué condiciones llegará a surgir la cooperación de egoístas no sometidos a una autoridad central?, enfatizando en el hecho de que “la cooperación existe y que la civilización está fundamentada en ella” (p.15).

El autor propone que la cooperación puede evolucionar en tres etapas:

(…) A partir de pequeños grupos apiñados que fundamenten su cooperación en el principio de reciprocidad, cuando una cierta proporción de sus interacciones se lleve a cabo con miembros de su mismo grupo, incluso aunque la proporción sea pequeña.
En el nudo de la historia en que una estrategia basada en la reciprocidad puede desenvolverse con éxito en un mundo donde se esté practicando un gran número de estrategias de diferentes tipos.
En el desenlace de la cooperación fundada en el que la reciprocidad puede desenvolverse con éxito en un mundo donde se estén practicando gran número de estrategias de diferente tipo, y que por así decirlo, los engranajes de la evolución social tienen un retén de enclavamiento. (p.31).

Para desarrollar su estudio sobre cooperación, Axelrod realizó dos torneos computarizados de dilema del prisionero iterado, enfatizando en lo común que es una situación de dilema de prisionero en distintas tipos de interacción social y en el hecho que “ en el dilema del prisionero iterado, la cantidad de cooperación lograda, así como la norma específica para alcanzarla, dependen de una amplia variedad de factores que guardan relación con el contexto del juego, las peculiaridades de los jugadores individuales y la forma de relación que estos tengan” (p.37).

El problema de la cooperación
La cooperación se puede definir como un conjunto de acciones o estrategias consientes e intencionadas realizadas por dos o más jugadores, donde no existe ninguna clase de subordinación y que optan por llegar a un máximo beneficio entre ellos sin que se organice una relación jerárquica entre los jugadores (Garcia, 1993).

Para la negociación es evidente que las personas impulsen su poder empleando gran cantidad de estrategias que favorezca a ellos, pero nunca piensan de manera colaborativa donde pueden sacar mayor beneficio de estos procesos; como bien plantean Ernst Fehr y Klaus M. Schmidt “existe una fuerte evidencia de que las personas explotan su poder de negociación en mercados competitivos pero no en situaciones de negociación bilateral”. Por ejemplo, cuando se participa en juegos de cooperación voluntaria, si en algún momento se presenta la oportunidad de castigar al compañero, aunque el castigo sea fuerte para el castigado, se mantiene la cooperación estable. (Fehr & Schmidt, 1999); con el fin de aprovechar situaciones que se presentan al momento de negociar.

El nivel de cooperación puede ser altamente mejorado en el juego del dilema del prisionero, ya que la estrategia depende del pago y le presta más atención a la influencia integral de los vecinos cercanos, la supervivencia de los jugadores obedece a la formación de los grupos de jugadores, existe una meta o un beneficio común entre jugadores que mejora el nivel de cooperación significativamente cuando se alcanza esta meta en común Resulta que el entorno económico determina si los tipos justos o los egoístas d o m i n a n e l comportamiento de equilibrio (Fehr & Schmidt, 1999).

Métodos

Se trató de un estudio descriptivo de tipo aplicado y de corte transversal. Se consideraron variables tanto cuantitativas como cualitativas. Para su realización, se desarrollaron entrevistas estructuradas a los jugadores expertos involucrados en la toma decisiones de los procesos de negociación del sector cacaotero de Palermo - Huila. En las citadas entrevistas, se le preguntó a los participantes sobre los aspectos relevantes que se presentan en los procesos de negociación entre los productores y acopiadores. Las entrevistas, se basaron en un cuestionario compuesto por preguntas abiertas, enmarcadas en categorías relacionadas con las diferentes variables de estudio y se enfocaron, en aspectos como los aspectos necesarios para que hubiese cooperación y las relaciones entre las partes. Se formuló una muestra determinística para la realización de las mismas. Además se hizo acto de presencia en una reunión entre cacaoteros y acopiadores en la cual se identificaron las actitudes estratégicas de los jugadores.

Para la realización del estudio, se optó por un modelo de dilema de prisionero iterado. La simulación consistió en un enfrentamiento de estrategias programadas, basadas en los resultados de las entrevista. (O actitudes estratégicas), de manera sucesiva, la cual se desarrolló por medio de un torneo computacional, tomando como base a Axelrod (1986) con el fin de determinar cuál actitud tenía un mejor rendimiento. Las puntuaciones arrojadas en la simulación son simbólicas y no están relacionadas con ninguna variable en concreto (rentabilidad, determinación de precios, etc.) representando sólo un valor abstracto que ayudó a determinar la estrategia más eficiente y la que mayor beneficio daría tanto a productores como acopiadores de cacao. Figura 2.

Figura 2.
Modelo metodológico. Fuente: elaboración Propia

Para la realización del modelo de dilema del prisionero iterado en el contexto de los procesos de cooperación del sector cacaotero del municipio de Palermo Huila, se realizaron aproximaciones de las actitudes estratégicas detectadas en las entrevistas de profundidad hechas a jugadores expertos y en el proceso de observación directa, y fueron modeladas, a su vez, en el Software Oyun, haciendo uso de autómatas de estancia finita. En la tabla 1, se describen las actitudes estratégicas.

Tabla 1. Descripción de las estrategias

Resultados

En la simulación de dilema del prisionero iterado que se realizó para modelar las posibles actitudes estratégicas, el pago individual por estrategia más alto fue de 5322 y el pago total de juego más elevado fue de 10644 (Figura 3). Estos resultados se dieron cuando los dos jugadores decidieron cooperar durante todo el juego y, por consiguiente, obtuvieron un pago R (recompensa por cooperar), que como ya se planteó anteriormente, es superior al pago P como al pago S.

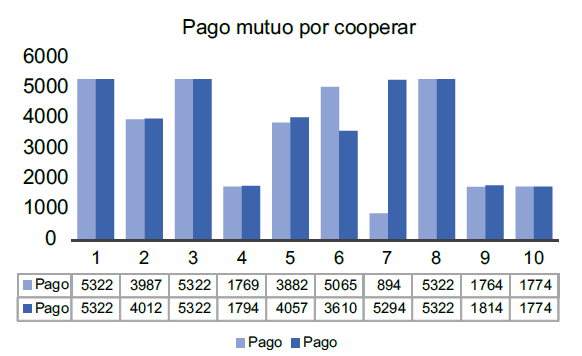
Figura 3.
Análisis de pago mutuo por cooperar. Fuente: Elaboración propia

Los resultados en los diversos enfrentamientos de las actitudes estratégicas (Tabla 2).

Tabla 2. Pagos del Torneo

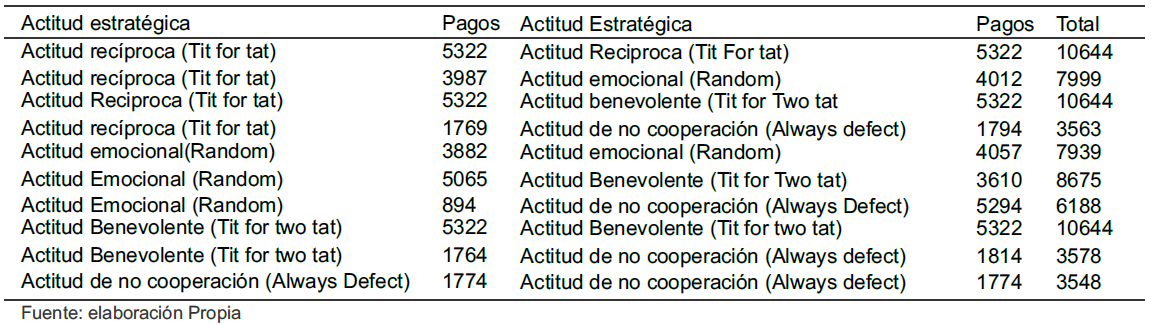
La situación de cooperación ideal se logró en tres juegos del torneo: cuando los dos jugadores tuvieron una actitud recíproca (jugaron Tit For Tat), cuando uno tuvo una actitud benevolente y su contraparte una actitud recíproca (Tit For Two Tit y Tit For Tat) y cuando, los dos jugadores jugaron de manera benevolente (jugaron Tit For Two Tat).

Por el contrario, los pagos más pobres se presentaron cuando un jugador tuvo una actitud recíproca y el otro una de negación a la cooperación (Tit For Tat y Always Defect), cuando un jugador jugo de manera benevolente y su contraparte de negó a cooperar (Tit For Two Tat Vs Always Defect) y cuando ambos jugadores tuvieron una actitud de negación a la cooperación (Always Defect y Always Defect), siendo este a la vez el juego que en general arrojo los pagos más bajos (sólo de 1774 para cada jugador) y exponiendo, en un proceso comercial entre cacaoteros productores y acopiadores, una actitud de negación a la cooperación, sería claramente la peor actitud estratégica en general.

Análisis comparativo de las estrategias.
En la tabla 3, se exponen los resultados individuales de las estrategias a lo largo del torneo de dilema de prisionero iterado.

Tabla 3. Resultados Individuales

Los resultados finales del torneo de Dilema del prisionero iterado desarrollado con el programa Oyun, (figura 4), dieron como ganadora a la actitud recíproca (estrategia Tit For Tat) en la que, como ya se explicó, consiste en lo siguiente: el jugador inicia cooperando y, seguidamente, responde de manera recíproca a la jugada del otro jugador. El Tit For Tat, tuvo una puntuación de 21722, mientras que la actitud benevolente (Tit For Two Tat) se situó en el segundo lugar, con una puntuación de 21340, el tercer lugar fue para la actitud emocional (estrategia aleatoria o Random) y el último lugar lo ocupó la actitud de nunca cooperar (Always Defect) la cual sólo tuvo una puntuación global de 12450, teniendo una diferencia negativa notable de 9272 con la estrategia que ocupo el primer lugar. Cabe aclarar nuevamente, que estos resultados son puramente simbólicos y no tienen relación con variables como precios, ingresos o similares.

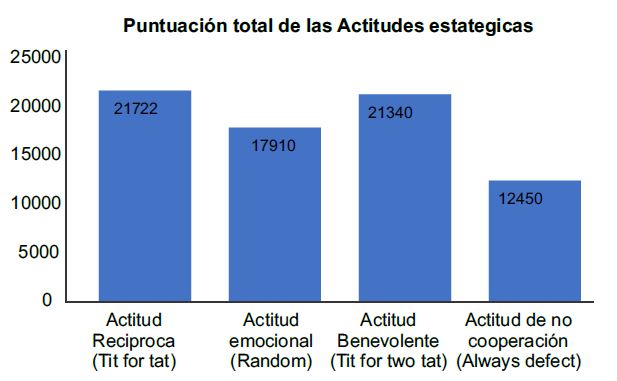
Figura 4.
Puntuacióntotaldelasactitudes estrategias. Fuente: elaboración propia

En resumen, torneo computarizado de dilema de prisionero, permite establecer que:

-Tanto para cacaoteros como para acopiadores es mejor presentar una actitud de cooperación, es decir, se debe cooperar desde un principio y buscar una cooperación continua a lo largo del juego.
-Practicar la reciprocidad da muy buenos resultados. Ambas partes deberían responder tanto a la cooperación, como a la no cooperación.
-Se deben generar actitudes estratégicas que faciliten la comunicación y las intenciones de cooperación con su contraparte.
-Tanto para productores como acopiadores de cacao, jugar de manera emotiva y azarosa, sin tener un criterio lógico de decisión y no establecer pautas de comunicación claras, ocasionaría malos resultados individuales y además, desfavorecían la negociación.
-Negarse a cooperar es, a mediano y largo plazo, una mala estrategia tanto para los productores como para los acopiadores. La simulación, concluye que las actitudes de cooperación ofrecen unos rendimientos (pagos a los jugadores) claramente superiores.

Conclusiones

La teoría de juegos nacida entre otros, por los aportes de Von Neumann y John Nash, ha sido usada en diversas disciplinas para el estudio, el análisis y la creación de modelos de competencia y cooperación.

Dada la complejidad en la cual viven inmersas las organizaciones comerciales, es importante desarrollar herramientas que permitan modelar su funcionamiento y sus características más inherentes y las interrelaciones entre estas.

El dilema del prisionero, una de las herramientas más conocidas dentro de la teoría de juegos, ha sido usada en estudios de diferentes áreas del conocimiento, para el análisis de estrategias competitivas y cooperativas de grupos de jugadores, ayudando a determinar las actitudes estratégicas más favorables.

Los resultados del experimento de Axelrod (1986) coinciden con los del presente estudio. Al realizarse una aproximación del dilema del prisionero en juegos iterados, las actitudes de cooperación, al largo plazo, dieron mejores resultados que las actitudes no cooperativas.

Los resultados del experimento, permitieron demostrar que si los cacaoteros y acopladores juegan de manera asarosa, sin planicación de acciones y sin una intención de cooperar desde un principio, tendrán resultados individuales comparativamente más bajos.

El torneo de dilema del prisionero iterado dio como ganadora a la actitud recíproca entre jugadores, por tanto, se entiende la necesidad de que exista entre los productores y acopiadores un comportamiento reciproco, cooperativo en el que haya una comunicación horizontal clara y en el que se busque constantemente un beneficio mutuo.

Se propone la necesidad de desarrollar de manera continua, entre los jugadores, reuniones formales y círculos de calidad que permitan una mayor eciencia negociación y que faciliten la cooperación continua entre las partes.

La aplicación de un modelo de teoría evolutiva de juegos en el contexto de los productores y acopiadores de cacao, permitió establecer que la formulación y ejecución de estrategias de cooperación, enmarcadas en la comunicación entre las partes, el mejoramiento de las relaciones y la reciprocidad, generará un benecio para los dos grupos en miras a un crecimiento continuo y a una mayor sostenibilidad del sector.

En este sentido, se entiende que aproximaciones de la computación al análisis de los patrones y dinámicas sociales, permiten, desde este nuevo enfoque, profundizar en el estudio de los factores, las interrelaciones y las sinergias propias de su naturaleza.